Ultrahigh Temperatures
Ultrahigh temperatures, those near and above roughly 3000°C, present an interesting problem to accurate pyrometry. The issues are related to calibration, interference, and inherent error. SpectroPyrometers enjoy advantages in these three areas that result in superior performance at ultrahigh temperatures.
Calibration
Problem:
In general, conventional pyrometers are calibrated by exposing them to temperatures within their designated range. In the simplest case, the instrument is exposed to the extremes: a temperature near the low end of the pyrometer’s range and one near the high. The instrument’s output is adjusted to be correct at those two values, and all others are interpolated or extrapolated.
The problem is that sources of known temperature and emissivity beyond 3000°C are rare and costly. Where they do exist, they are necessarily calibrated at a maximum of 2700°C (the upper temperature limit for the calibration of a radiation thermometer by NIST). This means that virtually all pyrometer measurements above 2700°C are based on extrapolation. Extrapolated measurements are less reliable than those that are interpolated, and extrapolation errors continue to grow with temperature.
Solution:
A spectrophotometric pyrometer (the original name of the SpectroPyrometer) has an advantage in calibration, and therefore in high temperature measurement. Calibration of a spectrophotometer is in radiance, or, more precisely, radiation intensity at a particular wavelength. The spectrophotometer can be calibrated throughout its entire range without being exposed to high temperatures. In fact, a spectrophotometer is completely calibrated on exposure to one known spectrum (one known temperature). SpectroPyrometers prove this fact routinely: they are calibrated at one temperature and tested throughout their temperature range. An example is shown in the table below.
| Standard, °C | Spectro-Pyrometer, °C | ΔT, °C | ΔT/T ±% absolute |
|---|---|---|---|
| 995.5 | 996.0 | 0.5 | 0.02 |
| 1198.1 | 1200.9 | 2.8 | 0.09 |
| 1492.1 | 1493.5 | 1.4 | 0.04 |
| 1982.6 | 1983.5 | 0.9 | 0.02 |
| 2184.0 | 2182.0 | 2.0 | 0.04 |
| averages | 1.5 | 0.04 |
Interference
Problem:
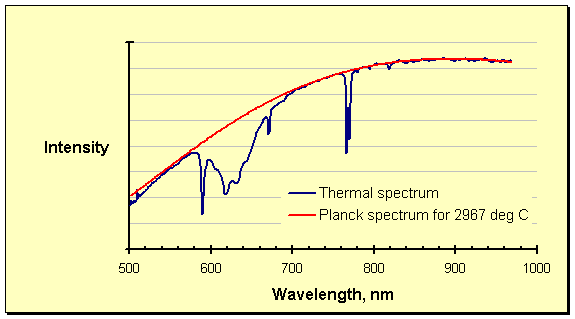
Interference from process offgas, epitomized in the spectrum above as the absorption between roughly 580 and 700 nanometers, has been described in detail elsewhere on these pages. The interference at these wavelengths visually overshadows that in the rest of the spectrum, which is by no means clean. The obvious dip at 760 – 780 nanometers is one case in point, but the entire spectrum is noisy. The absorption phenomenon worsens with increasing temperature; at ultrahigh temperatures it can affect huge sections of the thermal spectrum. Pressure enhances the interference, as might be expected, by packing more of the absorbing species into the optical path (the lines of absorption are also broadened by quantum effects). Carbon materials, especially graphite, are known to be sources of the absorbing species. At ultrahigh temperatures graphite is the refractory of choice, ensuring that such interference is widespread.
Solution:
The SpectroPyrometer detects and rejects areas of the thermal spectrum such as the ones shown at 580 – 700 and 760 – 780 nanometers. After the removal of this much of the thermal spectrum, there is still ample data to produce good temperatures. Accurate results have been seen with as much as 70% of the spectrum removed. The SpectroPyrometer also has good noise rejection, which insures that the remaining thermal spectrum is best used to generate an accurate temperature reading. The noise rejection of the SpectroPyrometer is shown in the table below. The ± values after the temperature are the tolerances, or limits of confidence for each temperature.
| Input | SpectroPyrometer Output, °C, with | |
| Temperature, °C | 5% noise added | 10% noise added |
| 1000 | 1001.6 ± 8.1 | 1001.8 ± 12.7 |
| 1400 | 1400.4 ± 6.6 | 1402.9 ± 6.7 |
| 1800 | 1799.1 ± 6.7 | 1801.8 ± 13.3 |
| 2200 | 2201.6 ± 2.8 | 2194.8 ± 17.2 |
| 2600 | 2600.6 ± 5.6 | 2607.3 ± 24.2 |
| 3000 | 3004.5 ± 8.4 | 2980.5 ± 31.6 |
| Average error: | 0.07% | 0.24% |
Inherent error
Problem:
The error analysis from Planck’s law shows that the error is proportional to the absolute temperature squared. Consequently, the uncertainty that causes an error of 2°C at 1000°C will cause an error of 6.4°C at 2000°C, and 13.2°C at 3000°C.
Solution:
Although there is no absolute solution for error increasing with temperature, the radiance calibration mitigates the problem to a large degree. The error analysis includes a multiplicative factor, dependent on both wavelength and temperature, which reduces the error in temperature that correlates to a given error in radiance. At 3000°C and for the extremes of wavelength of the SpectroPyrometer, a 1% uncertainty in radiance corresponds to a 0.4% uncertainty in temperature. In practice, temperature errors are found to be less than those predicted by the extremes of wavelength.
Analogy to explain extrapolation error
Imagine holding a straight rod parallel to the ground directly in front of you, with your arms a shoulder’s width apart. You support the rod loosely in the circle between each thumb and forefinger. Now your assistant comes along and wiggles the rod up and down as much as they can without breaking your grip. At any point between your hands the rod can’t move very much. The up-and-down excursion of the rod is analogous to the error in temperature caused by interpolation between two imperfectly-known end locations. Now slide one hand to the center of your body so that only one hand is near the end of the rod and the other is near its center. Your assistant again does their stuff. The excursion out near the unsupported end of the rod is now substantially greater, even though the circle of your fingers is the same (the temperatures are still known to the same imperfect accuracy). It’s clear that the farther you extend the length of the rod, the greater the uncertainty in the position of the end point becomes due to extrapolation. That is, the greater the difference between the temperature to be determined and the last calibration point of a conventional pyrometer, the larger the error.

